1 - תפיסת מרחק וגודל, אשליות וקביעויות
מתוך הקלטות ומצגות המנחה גיא שעשוע וחומרי הלימוד באתר הקורס
קלט ורמזים
- ניתן להניח כי המידע הבסיסי, ההתחלתי, שבו משתמשת מערכת התפיסה הוא תמונת העולם המתקבלת על רשתיות העיניים.
- אנו מניחים שמדובר במידע חסר, כיוון שההיטל על הרשתית הוא דו ממדי, אך תפיסת מרחק/עומק היא תלת ממדית.
- ניתן לחשב באופן מוחלט מה ההיטל הדו ממדי מתוך תמונה תלת ממדית, אך הפעולה לא עובדת להיפך.
- למשל בבואה דו ממדית של כדור יהיה עיגול, אך היטל עגול יכול להיות מטבע.
- יש לנו 2 תמונות דו ממדיות, אחת מכל עין והן אין זהות כיוון שכל עין ממוקמת בזווית שונה.
- רמזים חד עיניים אינם זקוקים לשתי העיניים, וגם לא לעומק אמיתי.
- מתוך רמזים חד עיניים לומדים את הרמזים הפיקטוריאליים, שיכולים להתקיים גם בתמונה דו ממדית (ציור, צילום וכדומה) של עולם תלת ממדי.
האתגר של תפיסת מרחק
איך לשחזר/להסיק את הממד השלישי (מימד העומק/המרחק) מתוך שתי התמונות הרשתיות הדו ממדיות?
רמזי מרחק
- נתונים דו ממדיים מהרשתית המשתמשים להסקת המרחק/עומק ויצירת ייצוג תלת ממדי
- ככל שיש יותר רמזי מרחק, תפיסת המרחק חדה יותר
- בכל מקרה, ייצוג המרחק הוא בקירוב ואינו מדויק
1 - גודל יחסי
רמז חד עיני
מוכרות הגודל
השוואה לגודל הצפוי
- מכונה גם גודל הדימוי הרשתי
- מבחינה אופטית, ככל שהעצם רחוק יותר, התמונה של על הרשתית קטנה יותר
- גודל העצם על הרשתית נעשה על ידי גודל הזווית שנוצרת ביחס לעין
- בעין יש קרנית, רוב המיקוד נעשה בה, והעדשה מבצעת חידודים
- הגודל הנראה של העצם הוא רמז לגבי המרחק
- ייתכן כי הדימוי הרשתי גדול יותר בגלל שהעצם גדול יותר, ולא בגלל שהוא קרוב יותר, לכן יש להצליב מידע עם רמזי מרחק אחרים.
- בהינתן מספר עצמים זהים, אשר שונים רק בגודלם, נוכל להעריך מי רחוק יותר לפי גודלם.
מוכרות הגודל
השוואה לגודל הצפוי
- השוואה של גודל הדימוי הרשתי של עצם לגודל הצפוי/המוכר של הדימוי הרשתי שלו.
- למשל גודל הדימוי הרשתי הצפוי של הפלאפון בכף היד.
- ככל שהדימוי הרשתי גדול יותר מהצפוי, נסיק שהוא קרוב יורת אלינו ביחס למרחקו הרגיל מאתנו.
- כשיחס הגדלים בין הדימויים של עצמים מוגרים שונה מהיחס המוכר לנו, ככל שעצם אחד יוצא קטן יותר מהצפוי ביחס לעצם שני, כל נמקם אותו רחוק יותר מאתנו מאשר השני.
- למשל אנו מכירים ולכן מצפים את יחסי הגודל בין כיסא לשולחן, לכן כשגודל השולחן גדול יותר מהכיסא על הרשתית, נדע עדין להעריך שהם באותו מרחק מאתנו
2 - הצללה
רמז חד עיני

מרחק הצל מהעצם שיוצר את הצל

- מדפוס ההצללה על פני עצמים המוח מסיק על המבנה תלת מימדי שלהם תוך שימוש בהנחות על מיקום מקור האור
- החלקים הבהירים יותר מפורשים כקרובים יותר, והחשוכים כרחוקים יותר/שקועים
- נטיית אור מלמעלה - יש לנו נטייה טבעית להניח שמקור האור מגיע מלמעלה, לרוב שמש, ירח, תאורה וכדומה
- נטיית עצמים בולטים - ייתכן שהמוח מפעיל הנחה נוספת שרוב הצורות צריכות להיות בולטות ביחס למשטח שטוח ולא שקועות בו, כך המצב לרוב בעולם. כשהתפיסה מתנגשת עם תפיסת האור מלמעלה ייתכן אפילו שנקבל תחושת עומק חלשה יותר.

מרחק הצל מהעצם שיוצר את הצל
- מהיחס שבין עצם לבין הצל שהוא מטיל על משטח/עצם אחר, ניתן להעריך את מרחק העצם מהמשטח
- אנו מפענחים את התמונה מתוך הנחה של מקור אור מסוים שמאיר את החלקים שבולטים לעומתו, ומצליל את החלקים שמוסתרים ממנו, ככל שהפרשנות דומה למה שקורה במציאות כך גם החוויה התלת ממדית משמעותית יותר.

3 - הסתרה חלקית
רמז חד עיני
עיקרון לפיו במידה לשני משטחים יש קו מתאר משותף, נשייך את הקו לאחד המשטחים, ומניחים שהמשטח השני מוסתר על ידו ולכן רחוק יותר.
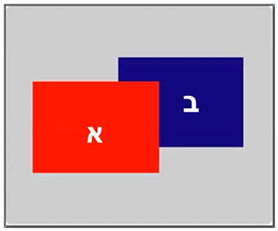
עיקרון לפיו במידה לשני משטחים יש קו מתאר משותף, נשייך את הקו לאחד המשטחים, ומניחים שהמשטח השני מוסתר על ידו ולכן רחוק יותר.

4 - פרספקטיבה קווית
רמז חד עיני

- כשאנו מביטים בקווים מקבילים, הם נראים כהולכים ומתקרבים זה לזה ככל שהם מתרחקים מאיתנו, עד שנפגשים בנקודה כלשהיא המכונה נקודת המגוז.
- ככל שעצם קרוב יותר לנקודת המגוז, הוא נתפס כרחוק יותר.

5 - דחיסות המרקם
רמז חד עיני
כאשר יש לנו משטח בעל מרקם אחיד, נניח שבאזורים בהם הפריטים קטנים וצפופים יותר, הם דחוסים יותר ורחוקים מהצופה.

כאשר יש לנו משטח בעל מרקם אחיד, נניח שבאזורים בהם הפריטים קטנים וצפופים יותר, הם דחוסים יותר ורחוקים מהצופה.

6 - גובה יחסי/קרבה לקו האופק
רמז חד עיני
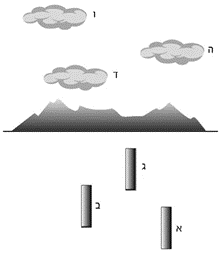
- כשהעצמים נמצאים מתחת לקו האופק, ככל שהם גבוהים יותר כך הם נתפסים כרחוקים יותר.
- כשהעצמים נמצאים מעל לקו האופק, ככל שהם נמוכים יותר כך הם נתפסים כרחוקים יותר.
- בהיעדר קו אופק ברור, אנו נוטים להניח שהוא מעלינו, לכן מה שגבוה יותר הוא רחוק יותר.
- בחלל סגור, ככל שהעצמים קרובים יותר בגובהם אל החלק האחורי ביותר שלו (הקיר האחורי) כך הם נתפסים רחוקים יותר מאיתנו.

7 – היסט תנועה
רמז חד עיני
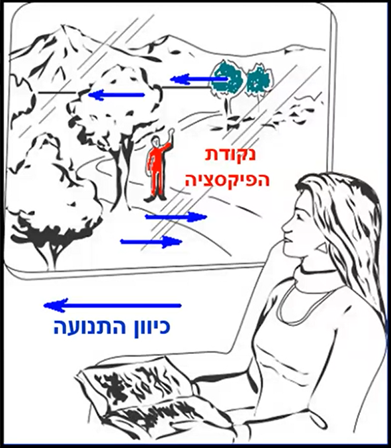
- אינו פיקטוריאלי
- כשמביטים החוצה מאובייקט בתנועה (למשל רכבת, מכונית וכו') ומתמקדים בנקודה אחת, המכונה נקודת הפיקסציה, ניתן לתאר את המהירות היחסית של העצמים סביב בהתאם לנקודה זו.
- כשנקודת הצפייה שלנו נעה, המוקד שבו מתמקדות עינינו ומה שסביבו באותו רחק מאיתנו – נשארים קבועים כלא זזים על הרשתית.
- כיוון התנועה – כל מה שנמצא בין הצופה לבין נקודת המיקוד, ינוע נגד כיוון התנועה של הצופה. מה שנמצא מעבר לנקודת המיקוד ינוע עם התנועה.
- מרחק העצמים –
- כשעצם "בורח"/"נע אחורה" על הרשתית, הוא נתפס כקרוב יותר אלינו מהמוקד, ככל שהוא נע אחורה מהר יותר כך הוא נתפס קרוב יותר אלינו.
- מה שנע בכיוון התנועה שלנו נתפס כרחוק יותר מאתנו מאשר המוקד.

8 – גודל הפער הדו עיני
- אנו מביטים על העולם עם שתי עיניים, וכל אחת במיקום מעט שונה מהשנייה, לכן מתקבלות שתי נקודות מבט שונות אשר מתלכדות יחד לתמונה אחת שנחווית כתלת ממדית.
- המרחק - ככל שהאובייקט יותר קרוב, הפער בין שתי העיניים גדול יותר. אם קרוב מידי אפילו נראה כפול למשל כשמקרבים מאוד את האצבע בין העיניים
- שדות הראייה של שתי העיניים ברובם חופפים, רק קצת בפריפריה רואים רק באחת מהן.
- הרמז מוגבל במרחק, אינו רלוונטי למרחקים גדולים
- הסבר הישרדותי - אנו נחשבים בטבע חיות טורפות, לכן שדה הראייה שלנו מתאים לתפיסת מטרה קרובה יחסית אלינו, אין צורך ביותר מכך. לעומת זאת חיה נטרפת כמו זוחלים, העיניים רחוקות יותר ואף בצדדים מנוגדים של הראש, על מנת לכסות יותר שדה ראיה ולהגן על עצמה מטורפים.
חוק אמרט – תיקון גודל ע"י מרחק
- קביעות הגודל – עצם שנמצא במרחקים שונים מאתנו, ייתפס באותו גודל למרות שגודל הדימוי הרשתי שלו משתנה עם מרחקו.
- גודל הדימוי הרשתי קטן ככל שהעצם מתרחק מאתנו, לכן כדי לתפוס נכון את גודל העצם צריך לתקן את גודל הדימוי הרשתי על פי המרחק.
- גודל נתפס = גודל דימוי רשתי X מרחק נתפס
- המידע שיש לנו בהתחלה, הוא גודל דימוי רשתי, אם אנחנו יודעים להעריך נכון את המרחק שלנו נוכל למעשה לשחזר את הגודל של העצם.
גודל הדימוי על הרשתית | המרחק הנתפס | גודל נתפס | |
|---|---|---|---|
אובייקט מתקרב פי X | גדל פי X | קטן פי X | קבוע |
אובייקט מתרחק פי X | קטן פי X | גדל פי X |
אשליות גיאומטריות של גודל עצמים
הנובעות מטעויות בתפיסת המרחק
- גודל העצם על הרשתית – אינו תלוי ברמזים ולכן חסין מטעויות.
- המרחק הנתפס – מתבסס על רמזי המרחק ולכן יכול להיות שגוי, מה שמוביל לגודל נתפס שגוי.
- אשליה של גודל נתפס – נובעת תמיד מטעות של המרחק הנתפס
1 - אשליית פונזו
- אורך הקווים זהה במציאות, אך נתפסים כשונים ביחס למיקום על שני הפסים השחורים.
- גודל הקווים על הרשתית – זהה
- המרחק הנתפס – הקווים האלכסוניים, מיצרים חוויה כמו קווים מקבילים שנמשכים לעומק, לכן לפי רמז הפרספקטיבה הקווית במרחק הנתפס, הקו שממוקם בחלק העליון של האלכסונים נראה רחוק יותר ולכן ארוך יותר.

2 - אשליית הירח
- כשהירח קרוב לקו האופק, הוא נדמה לנו כעצום
- גודל הירח על הרשתית – זהה
- המרחק הנתפס – רמזים כגון פרספקטיבה קווית, גובה יחסי, הסתרה, גורמים לתפיסת המרחק של הירח כרחוק יותר, ולכן לפי תיקון הגודל הוא נתפס כגדול יותר. לעומת כשהוא נמצא בגובה השמיים ואין רמזים סביבו, ונדמה קטן יותר
3 – אשליית מילר-לייר
- הקו השמאלי נדמה כקצר יותר מהימני על אף שהם זהים באורכם
- גודל הירח על הרשתית – זהה
- הסבר אפשרי – הקו עם הכנפיים הפתוחות נתפס אזור הרחוק בפינה שקועה. הקו עם הכנפיים הסגורות נתפס כאזור הקרוב בפינה בולטת. לכן תיקון הגודל ע"פ המרחק של הדימויים הרשתיים השווים של שני הקווים שוויה האורך, גורם לקו עם הכנפיים הפתוחות להיתפס גדול/ארוך יותר, אותו דימוי רשתי מוכפל במחק גדול יותר.
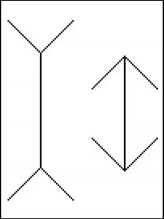
קשיים להסבר קביעות הפרספקטיבה
קביעות הפרספקטיבה אינה מסבירה במלואה את האשליות שהוצגו.
למשל אם מציגים את אשליית מילר-לייר בקווים מחוברים:
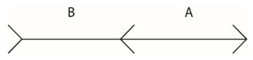 קשה לבסס את האשליה על כך שהנבדקים מייחסים מרחק גדול יותר לקו עם הכנפיים הפתוחות, שהרי שני הקווים באיור זה מחוברים לקו המשכי אחד.
קשה לבסס את האשליה על כך שהנבדקים מייחסים מרחק גדול יותר לקו עם הכנפיים הפתוחות, שהרי שני הקווים באיור זה מחוברים לקו המשכי אחד.למשל בקווים הבאים:
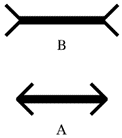 הקושי להסבר הוא העובדה שהנבדקים מדווחים שהקו עם הכנפיים הפתוחות (B) צר יותר בפועל.
הקושי להסבר הוא העובדה שהנבדקים מדווחים שהקו עם הכנפיים הפתוחות (B) צר יותר בפועל.לפי הסבר קביעות הפרספקטיבה, קו B נתפס במרחק גדול יותר מאיתנו, והתיקון היה אמור להגדיל את גודלו ורוחבו, אך בפועל נתפס כצר יותר.
4 – אשליית חדר איימס
בצד שמאל
בצד ימין
מבנה החדר
הסבר
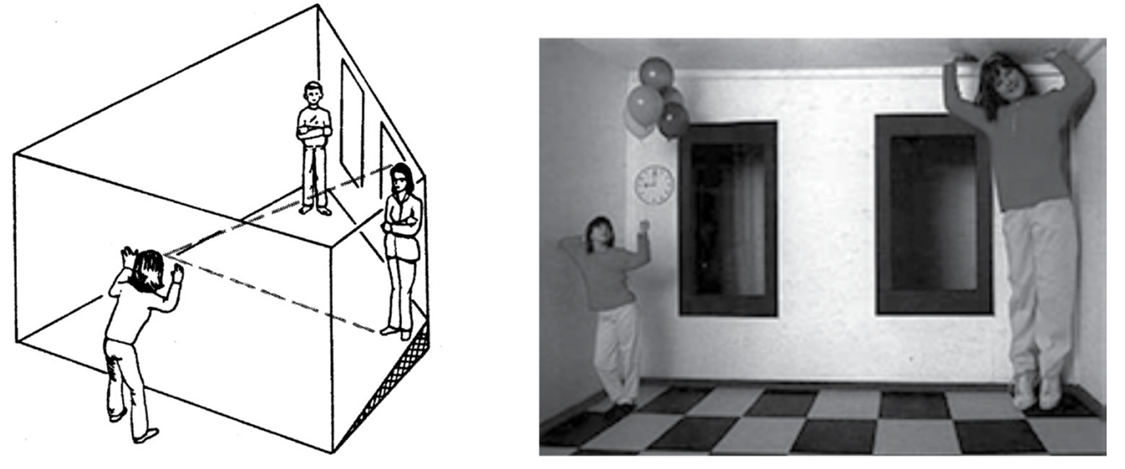
- סכמה של החדר בצורת טרפז שבנה איימס.
- שתי הדמויות בפינות זהות בגודלן
- הפינה השמאלית של החדר רחוקה יותר מהצופה.
בצד ימין
- התמונה כפי שרואה אותה הצופה, המתבונן בחדר בעין אחת דרך הפתח הצר
- האשליה - הדמות העומדת בפינה הימנית נראית גדולה בהרבה מן הדמות שניצבת בפינתו השמאלית.
מבנה החדר
- הפינה השמאלית של החדר רחוקה מעינו של המתבונן במידה רבה יותר מזו של הפינה הימנית.
- הגובה מן הרצפה לתקרה וגודלם וצורתם של החלונות עוותו כדי שהחדר ייתפס על ידי הצופה כחדר רגיל בצורה מלבנית , כלומר שהצופה ייחס לשתי הפינות מרחק שווה ממנו
הסבר
- כאשר הצופה מתבונן בחדר בעין אחת דרך העינית, כיוון שהדמות בפינה השמאלית מרוחקת מהצופה יותר מהדמות בפינה הימנית, הדימוי הרשתי שיוצרת הדמות השמאלית קטן באופן משמעותי מן הדימוי הרשתי של הדמות הימנית.
- בגלל העיוותים שבחדר, מוחו של הצופה בחדר מייחס לשתי הדמויות מרחק שווה, ולכן אינו מבצע הגדלה משמעותית יותר של הדימוי הרשתי של הדמות המרוחקת יותר, כפי שהיה צריך לעשות על פי תיקון הגודל על פי המרחק.
- לכן שתי הדמויות בחדר נתפסות על פי יחסי הגודל שלהן בתמונה על הרשתית, והדמות הרחוקה יותר שיוצרת דימוי רשתי קטן יותר נתפסת קטנה יותר.
- אפילו אם הדמות נעה מפינה אחת בחדר לשנייה, היא נתפסת כמתנפחת או מתכווצת.

שאלה 1
מדוע גודלו הנתפס של אובייקט המתקרב אלינו נשאר קבוע, לפי תיקון הגודל על פי המרחק הנתפס וקביעות הגודל?
- כי הדימוי הרשתי שלו נשאר בגודל קבוע, למרות השינוי במרחקו.
- כי המרחק התפס שלו קטן באותו יחס שבו גדל הדימוי הרשתי שלו.
- כי המרחק הנתפס שלו גדל באותו יחס שבו גדל הדימוי הרשתי שלו.
- כי הדימוי הרשתי שלו קטן באותו יחס שבו קטן המרחק שלו.
שאלה 2
אם פיסת המרחק שלנו מעריכה את המרחק של עצם מאתנו, כקטן (קרוב) מכפי שהוא באמת, סביר להניח שכתוצאה מכך נתפוס אותו –
- גדול מכפי שהיינו תופסים אותו אילו הערכנו את מרחקו בצורה נכונה.
- קטן מכפי שהיינו תופסים אותו אילו הערכנו את מרחקו בצורה נכונה.
- בגודל הנכון בגלל מנגנון קביעות הגודל.
- כנמצא במיקום קבוע בגלל קביעות המיקום.
תשובות
שאלה | תשובה |
|---|---|
1 | 2 |
2 | 2 |
