פרק 10 - רווח סמך ובדיקת השערות על תוחלת באוכלוסיה
סולמות
- שמי - נומינלי
- סדר - אורדינלי
- רווח - אינטרוולי
- מנה - יחס
מושגים סטטיסטיים באנגלית
משתנה | Variable |
נתונים | Data |
שכיח | Mode |
חציון | Median |
ממוצע מדגם | Mean |
אחוזון | Precentile |
אומד לסטיית תקן | std. Deviation |
טעות התקן | std. Error Of Mean |
שונות | Variance |
ציון תקן | Standardized |
אמידה
ניסיון להעריך גודל של פרמטר באוכלוסייה באמצעות מדד מהמדגם
דרישות לאומד טוב
חסר הטייה
לא מוטה כלפי מעלה או מטה. שבממוצע האומד יתן לנו את הפרמטר
שונות מינימלית
אם יש מספר אומדים מתאימים, נעדיף את האומד בו השונות מינימלית
לא מוטה כלפי מעלה או מטה. שבממוצע האומד יתן לנו את הפרמטר
שונות מינימלית
אם יש מספר אומדים מתאימים, נעדיף את האומד בו השונות מינימלית
אמידה באמצעות רווח/טווח ערכים
מסתמכת על האומד הנקודתי ובונה סביבו טווח סימטרי, ניתן יהיה לתת אחוזי ביטחון שהפרמטר אכן מצוי בתוך הטווח
לדוגמא
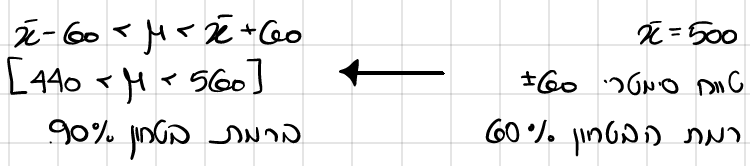
לדוגמא

רווח סמך לתוחלת כאשר סטיית תקן באוכלוסייה ידועה
נוסחת רווח סמך
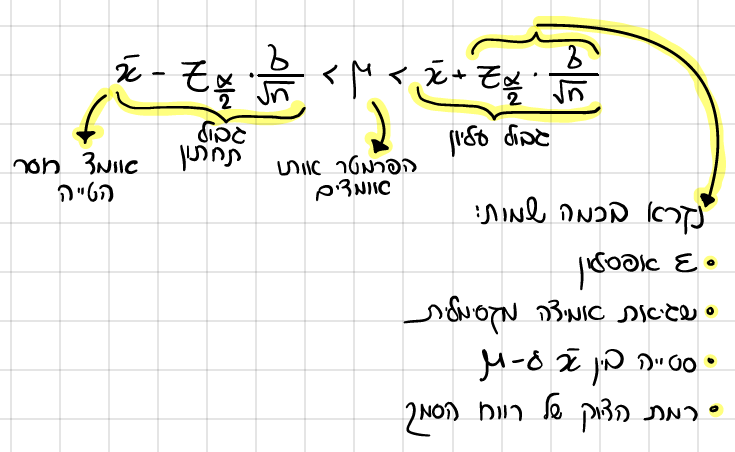
אפסילון
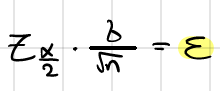
גודל מדגם
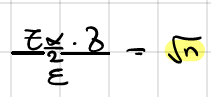

אפסילון
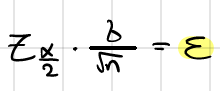
גודל מדגם
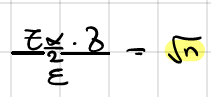
רמת בטחון ברווח סמך
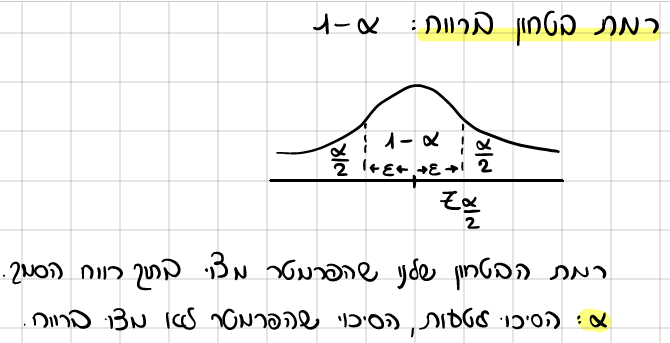
אורך רווח סמך
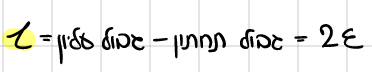
תרגיל - דיאטה
חוקר מעוניין לבדוק את ההשפעה של דיאטה חדשה על רמת הסוכר בדם. ידוע כי מספר מיליגרם הסוכר בדם בסמ"ק הוא מ שתנה מקרי שמתפלג נורמלית עם סטיית תקן 9.8 מ"ג. במדגם מקרי של 100 נבדקים שניזונו מהדיאטה זו נמצא שממוצע מיליגרם הסוכר בסמ"ק בדם שלהם היה 98.3.
טבלת נתונים
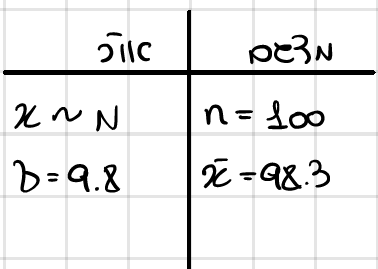
בנה רווח סמך לתוחלת רמת הסוכר בדם אצל הניזונים מדיאטה זו ברמת סמך 95%
ידוע כי תוחלת רמת הסוכר בדם באוכלוסיה כולה היא 100 מ"ג לסמ"ק. האם לדעתך ניתן להסיק שהדיאטה משפיעה על רמת הסוכר על סמך רווח הסמך שבנית בסעיף א'?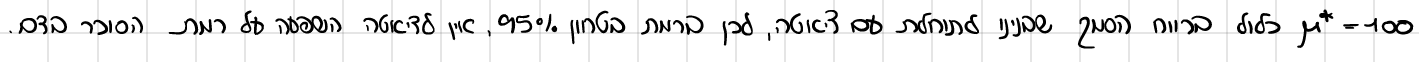
בהמשך לסעיף ב', מה תהיה מסקנת ברמת סמך של 90% ו-99%? הסבר עבור על אחד בנפרד, ללא חישוב.
טבלת נתונים

בנה רווח סמך לתוחלת רמת הסוכר בדם אצל הניזונים מדיאטה זו ברמת סמך 95%

ידוע כי תוחלת רמת הסוכר בדם באוכלוסיה כולה היא 100 מ"ג לסמ"ק. האם לדעתך ניתן להסיק שהדיאטה משפיעה על רמת הסוכר על סמך רווח הסמך שבנית בסעיף א'?
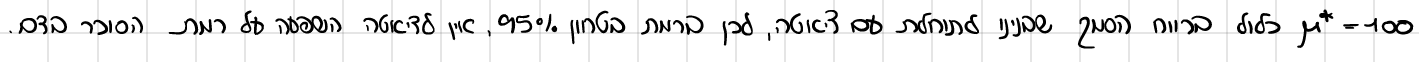
בהמשך לסעיף ב', מה תהיה מסקנת ברמת סמך של 90% ו-99%? הסבר עבור על אחד בנפרד, ללא חישוב.

תרגיל - שקיות סוכר
משקל שקיות מתוצרת בתי חרושת "סוכרי" הוא בעל התפלגות נורמלית עם סטיית תקן 10 גרם. כדי לבדוק אם תוצרת בית החרושת עומדת בדרישות התקן של המשקל הממוצע של כל שקית שאמור להיות 1 "ג, הוצא מדגם מקרי מתוצרתו.
מה צריך להיות גודל המדגם המינימלי כדי שאורך רווח הסמך למשקל הממוצע של שקית לא יעלה על 4 גרם ברמת סמך 95%?
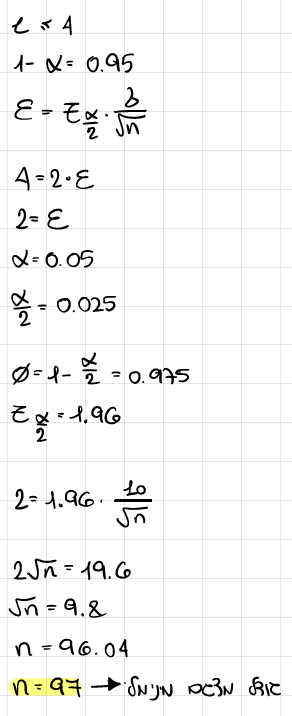
הוצא מדגם מקרי, ,שאת גודלו מצאת בסעיף א', והתקבל משקל ממוצע של 1.078 ק"ג. מצא רב"ס למשקל הממוצע של שקיות מתוצרת בית החרושת הנ"ל, באותה רמת ביטחון.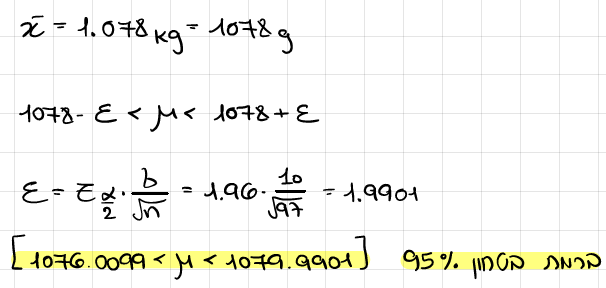
היצרנית טוענת שהשקיות בבית החרושת עומדות בדרישת התקן. האם ניתן לאשש את טענתה על סמך הרווח שמצאת בסעיף ב'? נמק מסקנתך.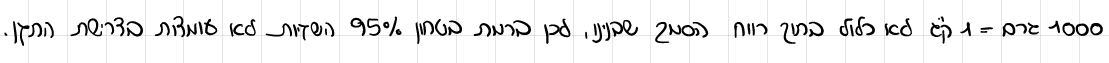
מה תהיה מסקנת ברמת ביטחון 90%? נמק אם ניתן להגיע למסקנה ללא חישוב.
בהנחה שהמשקל הממוצע התקני של שקיות הסוגר אמור להיות לפחות 1ק"ג, האם תשתנה מסקנתך בסעיף הקודם? הסבר מה תהיה מסקנתך
חוקרת דגמה 100 שקיות סוכר, קיבלה רווח סמך (1002,10008). באיזו רמת סמך השתמשה החוקרת?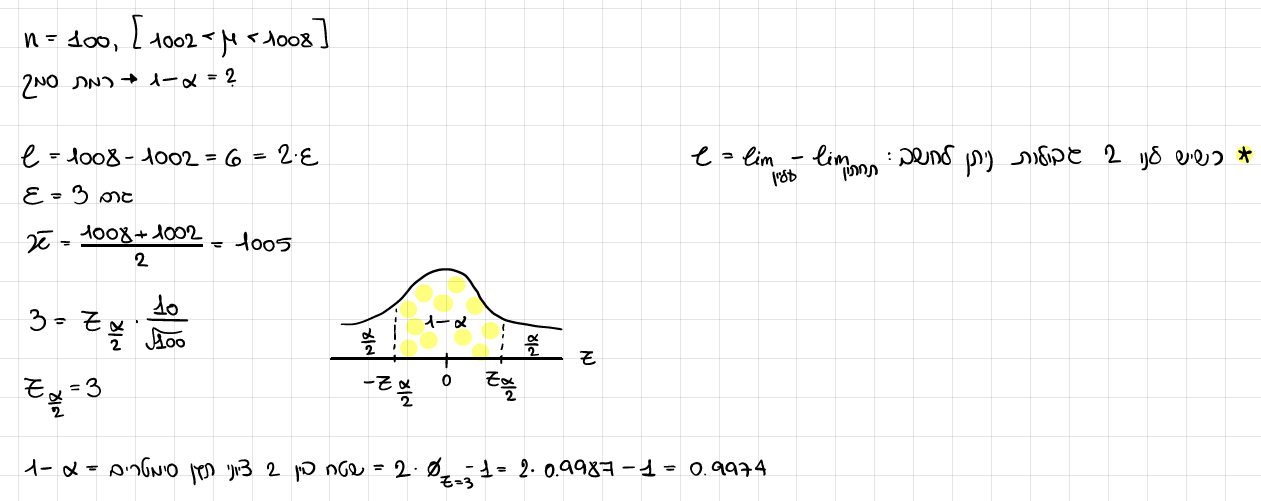
מהו גודל המדגם המינימלי של החוקר לדגום אם ברצונו שהסטייה בין האומד לפרמטר לא תעלה על 2 גרם ברמת ביטחון של 98%? השוו תוצאה זו לסעיף א'. מה ניתן להסיק?
מה צריך להיות גודל המדגם המינימלי כדי שאורך רווח הסמך למשקל הממוצע של שקית לא יעלה על 4 גרם ברמת סמך 95%?
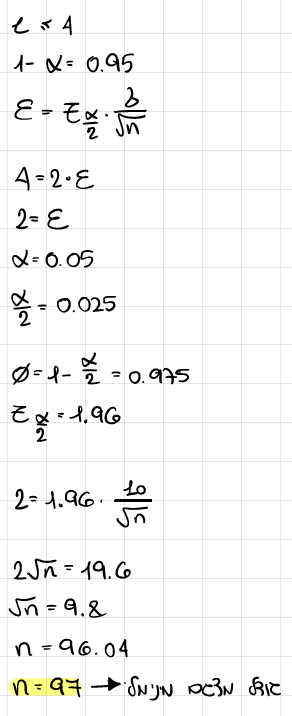
הוצא מדגם מקרי, ,שאת גודלו מצאת בסעיף א', והתקבל משקל ממוצע של 1.078 ק"ג. מצא רב"ס למשקל הממוצע של שקיות מתוצרת בית החרושת הנ"ל, באותה רמת ביטחון.
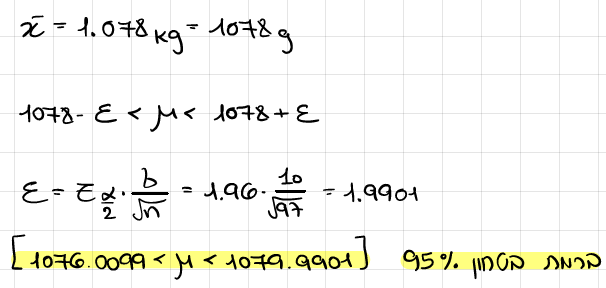
היצרנית טוענת שהשקיות בבית החרושת עומדות בדרישת התקן. האם ניתן לאשש את טענתה על סמך הרווח שמצאת בסעיף ב'? נמק מסקנתך.
מה תהיה מסקנת ברמת ביטחון 90%? נמק אם ניתן להגיע למסקנה ללא חישוב.

בהנחה שהמשקל הממוצע התקני של שקיות הסוגר אמור להיות לפחות 1ק"ג, האם תשתנה מסקנתך בסעיף הקודם? הסבר מה תהיה מסקנתך

חוקרת דגמה 100 שקיות סוכר, קיבלה רווח סמך (1002,10008). באיזו רמת סמך השתמשה החוקרת?

מהו גודל המדגם המינימלי של החוקר לדגום אם ברצונו שהסטייה בין האומד לפרמטר לא תעלה על 2 גרם ברמת ביטחון של 98%? השוו תוצאה זו לסעיף א'. מה ניתן להסיק?

מה משפיע על אורך הרווח ?
- שונות ← יחס ישר
- רמת ביטחון ← יחס ישר
- גודל מדגם ← יחס הפוך
5 שלבים בבדיקת השערות
- ניסוח השערות
- תנאים והנחות
- ציור התפלגות וכלל הכרעה
- חישוב סטטיסטי המדגם
- החלטה ומסקנה
1 - ניסוח השערות
תמיד ננסח את צמד ההשערות על הפרמטר באוכלוסיה, לא של המדגם.
H0
השערת הבסיס
השערה שמרנית, תמיד יהיה בה שוויון והיא מציגה מצב קיים, ללא שינוי.
H1
השערה אלטרנטיבית
השערת החוקר, תמיד השערה על עלייה, ירידה, שינוי או ללא שיוויון.
נתוני המדגם לא יכנסו להשערות ולא ישפיעו על כיוון ההשערה.
H0
השערת הבסיס
השערה שמרנית, תמיד יהיה בה שוויון והיא מציגה מצב קיים, ללא שינוי.
H1
השערה אלטרנטיבית
השערת החוקר, תמיד השערה על עלייה, ירידה, שינוי או ללא שיוויון.
נתוני המדגם לא יכנסו להשערות ולא ישפיעו על כיוון ההשערה.
2 - פירוט תנאים והנחות
- מדגם מקרי
- שונות ידועה/לא ידועה
- גודל מדגם מעל 30 או קטן מ30 ומתפלג נורמלי
3 - ציור וכלל הכרעה
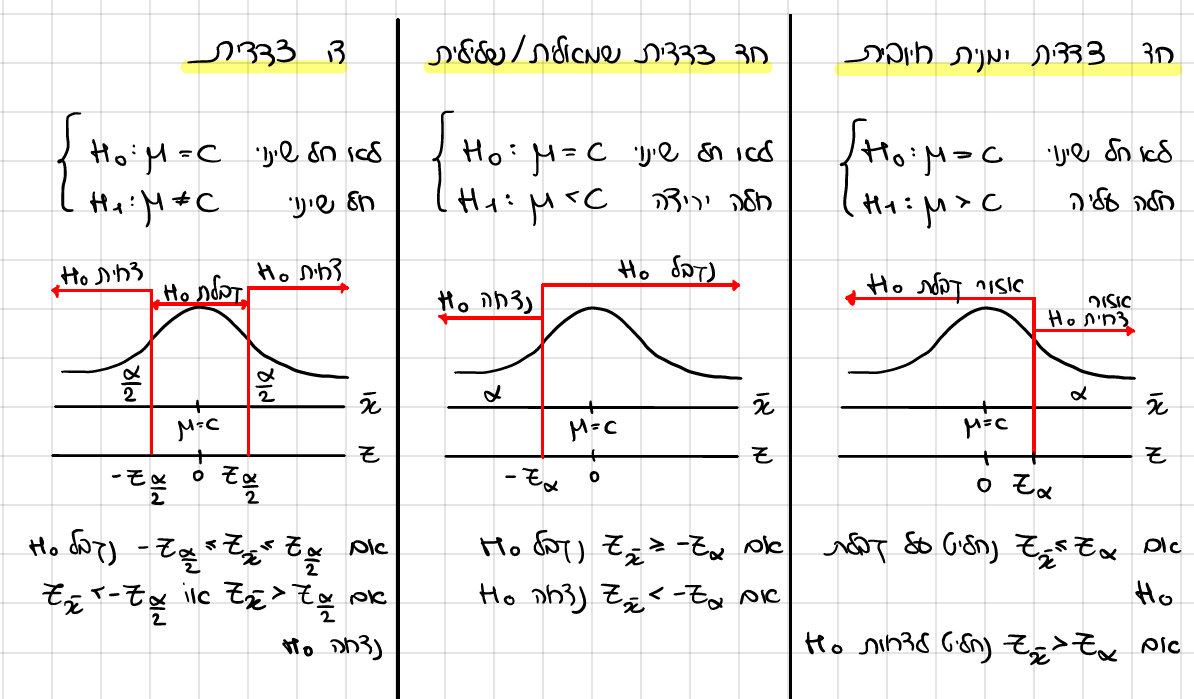
4 - חישוב סטטיסטי המדגם
חישוב לפי ציון תקן רלוונטי
5 - החלטה ומסקנה

תירגול - חיסכון למשפחה
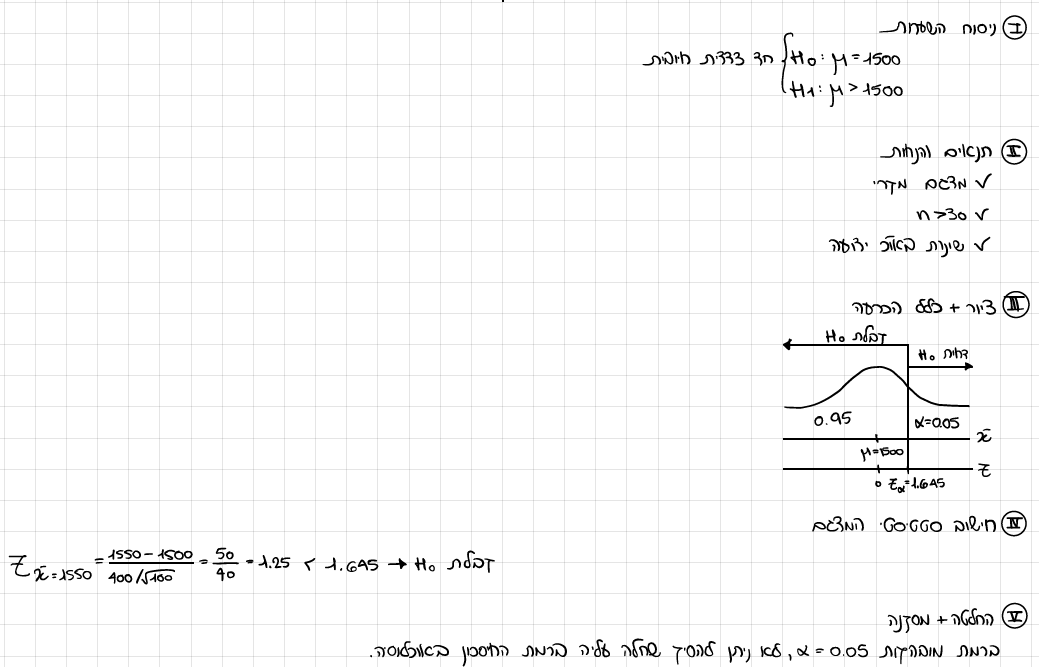
על פי נתוני הלשכה לסטטיסטיקה, רמת החיסכון הממוצעת למשפחה בישראל היא 1500 ש"ח לחודש עם סטיית תקן 400 ש"ח.
במדגם מקרי של 100 משפחות התקבל חיסכון ממוצע של 1550.
מנהל חברת השקעות טוען כי רמת החיסכון הממוצעת באוכלוסיה עלתה.
האם תוצאות המדגם מאוששות את טענתו?
בדוק ברמת מובהקות של 0.05.
טבלת נתונים
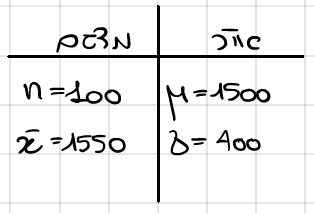
פתרון:
במדגם מקרי של 100 משפחות התקבל חיסכון ממוצע של 1550.
מנהל חברת השקעות טוען כי רמת החיסכון הממוצעת באוכלוסיה עלתה.
האם תוצאות המדגם מאוששות את טענתו?
בדוק ברמת מובהקות של 0.05.
טבלת נתונים

פתרון:

PV
הסיכוי לקבל תוצאה במדגם ותוצאות קיצוניות ממנה כאשר H0 נכונה.
הסיכוי לטעות מסוג 1, הסיכוי שנחליט לדחות את H( על סמך התוצאה במדגם, כאשר H0 בעצם נכונה.
איך מחשבים?
נחשב ציון תקן לתוצאה במדגם ונמצא שטח קיצוני לה
הסיכוי לטעות מסוג 1, הסיכוי שנחליט לדחות את H( על סמך התוצאה במדגם, כאשר H0 בעצם נכונה.
איך מחשבים?
נחשב ציון תקן לתוצאה במדגם ונמצא שטח קיצוני לה
תירגול - ממוצע ציוני בגרות
ממוצע ציוני הבגרות במתמטיקה בארץ בשנה מסוימת היה 7.9 עם סטיית תקן 1.2.
מדגם 100 בוגרי בי"ס תיכון מסוים השיג באותה שנה ממוצע של 7.6 בבגרות במתמטיקה.
טבלת נתונים:
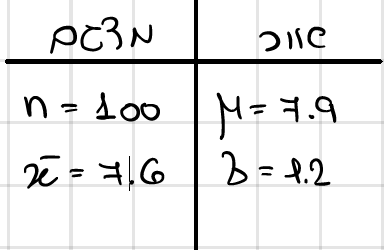
האם אפשר לטעון שבאוכ' בי"ס זה נמצאה ירידה שאיננה מקרית בהשוואה לממוצע הארצי ברמת מובהקות 0.05?

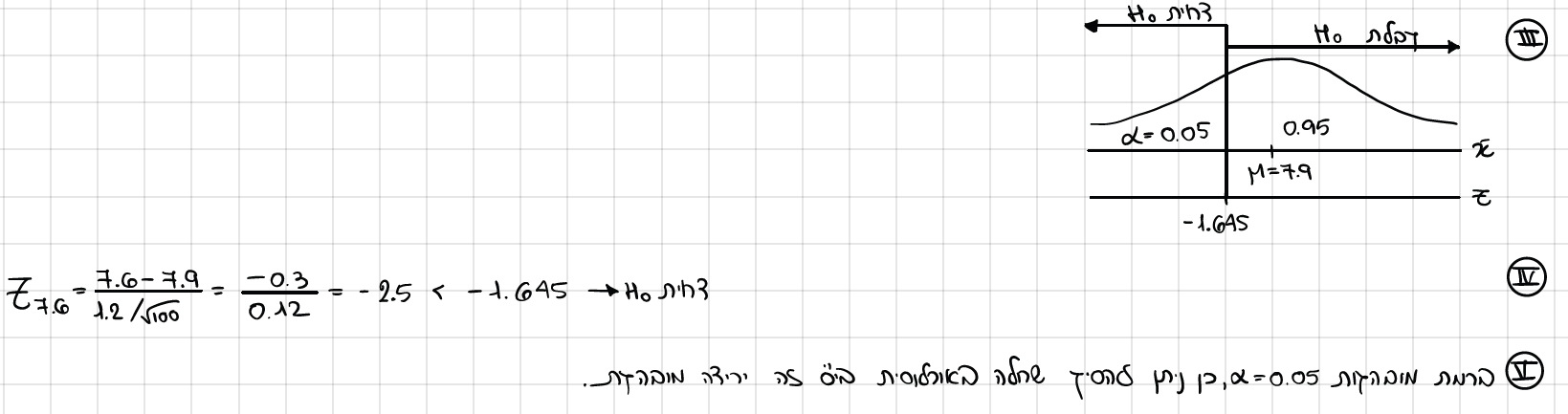
מהי רמת המובהקות הקטנה ביורת בה נחליט שחלה ירידה מובהקת בציונים?

מדגם 100 בוגרי בי"ס תיכון מסוים השיג באותה שנה ממוצע של 7.6 בבגרות במתמטיקה.
טבלת נתונים:
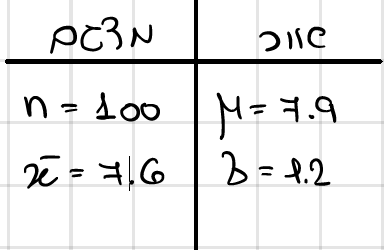
האם אפשר לטעון שבאוכ' בי"ס זה נמצאה ירידה שאיננה מקרית בהשוואה לממוצע הארצי ברמת מובהקות 0.05?

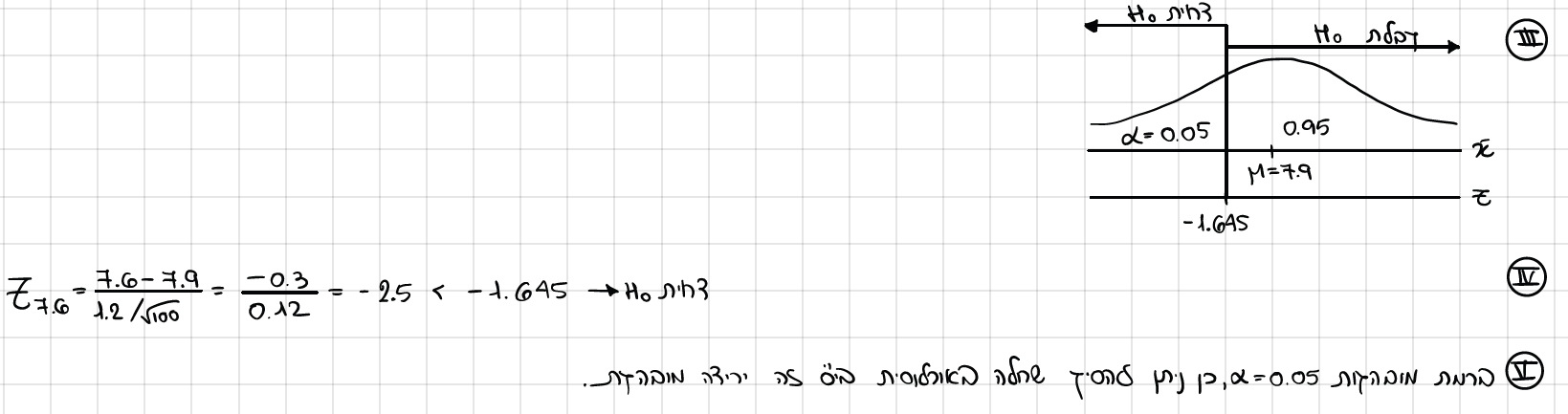
מהי רמת המובהקות הקטנה ביורת בה נחליט שחלה ירידה מובהקת בציונים?

תירגול - ציונים במבחן
ציונים במבחן יציריות מתפלגים נורמלית עם ממוצע 84 ושונות 15.
16 נבדקים קיבלו סם נבדק ביצועם תחת השפעותו, נמצא ממוצע 81.2 אצלם.
טבלת נתונים
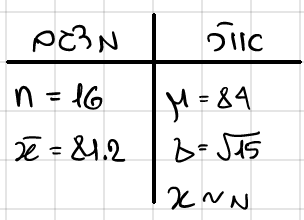
האם התוצאות מעידות על השפעה מובהקת של הסם על הביצוע בר"מ 0.01?
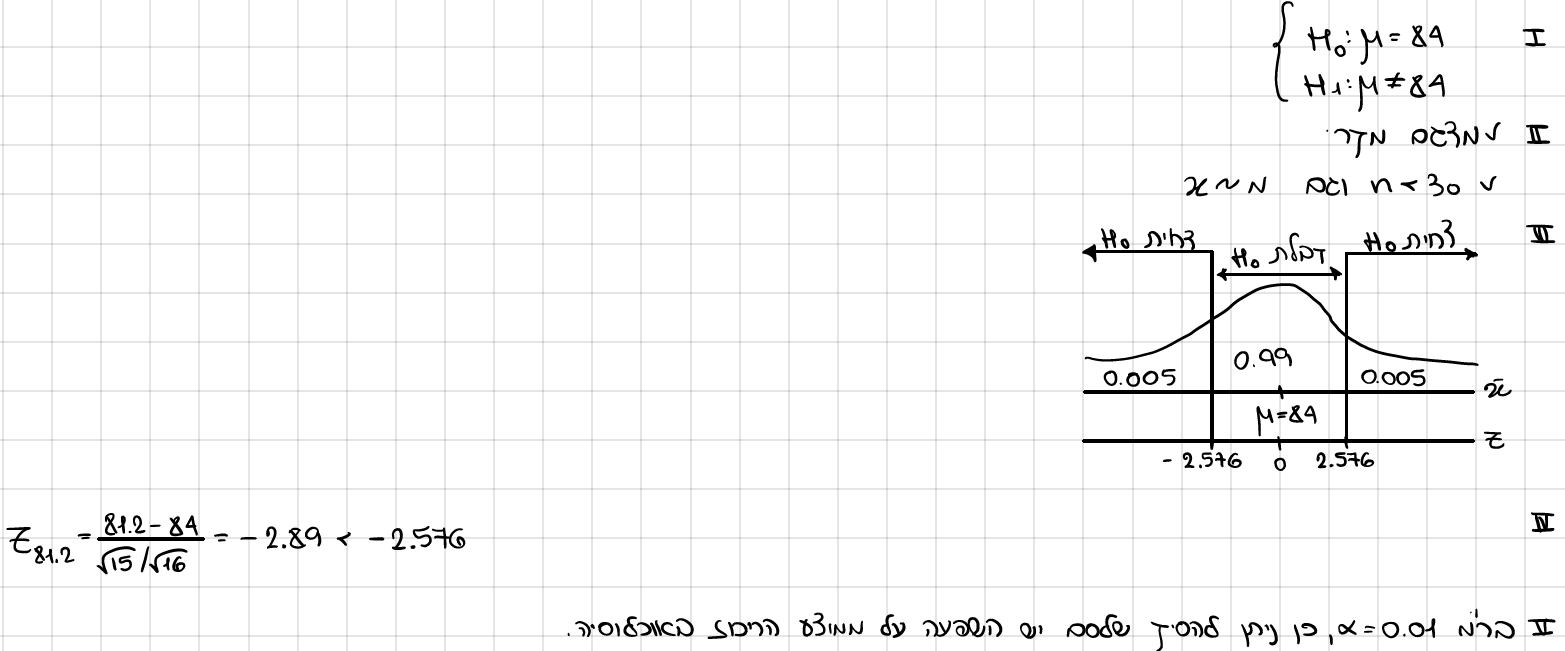
האם ניתן להסיק על סמך סעיף א ללא חישוב שהסם פוגע בביצוע באוהת ר"מ? נמק.

16 נבדקים קיבלו סם נבדק ביצועם תחת השפעותו, נמצא ממוצע 81.2 אצלם.
טבלת נתונים

האם התוצאות מעידות על השפעה מובהקת של הסם על הביצוע בר"מ 0.01?

האם ניתן להסיק על סמך סעיף א ללא חישוב שהסם פוגע בביצוע באוהת ר"מ? נמק.

תיאור גרפי של טעויות בהשערות
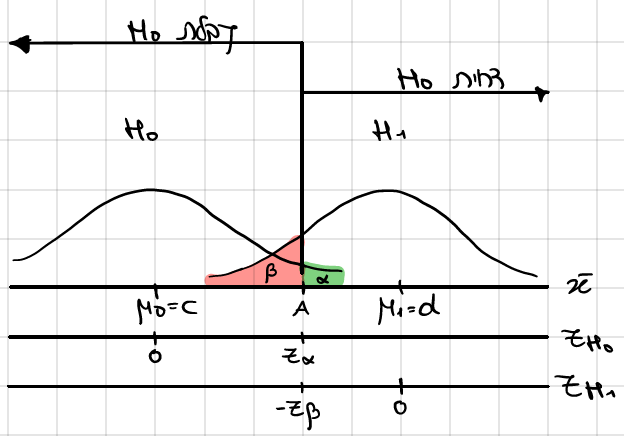
סוגי טעויות
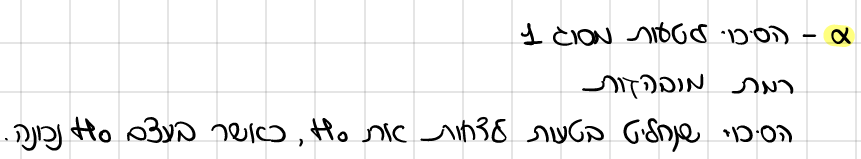
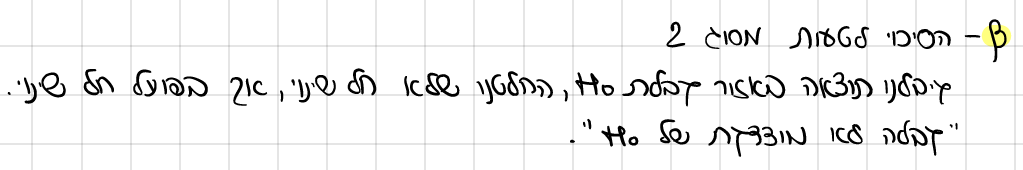
איך יודעים איזה טעות אנחנו מחפשים ?
החלטת החוקר | |||
קבלת H0 | דחיית H0 | ||
מצב בעולם | H0 נכונה | 1-a אין טעות קבלת מוצדקת של H0 חוקרת החליטה לקבל את H0 והיא אכן נכונה | a יש טעות דחיה לא מוצדקת של H0 החוקרת דחתה H0 אבל H0 נכונה טעות מס' 1 |
H0 לא נכונה | 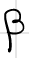 יש טעות יש טעותקבלה לא מוצדקת של H0 החוקרת לא הצליחה לגלות שחל שינוי | 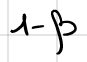 אין טעות דחיה לא מוצדקת של H0 עוצמת המבחן הסיכוי שהחוקרת כן תצליח לגלות שחל שינוי | |
3 שלבים לחישוב טעות מסוג 2
1 - מציאת A
כלל ההכרעה בציוני גלם לפי H0 ו-a
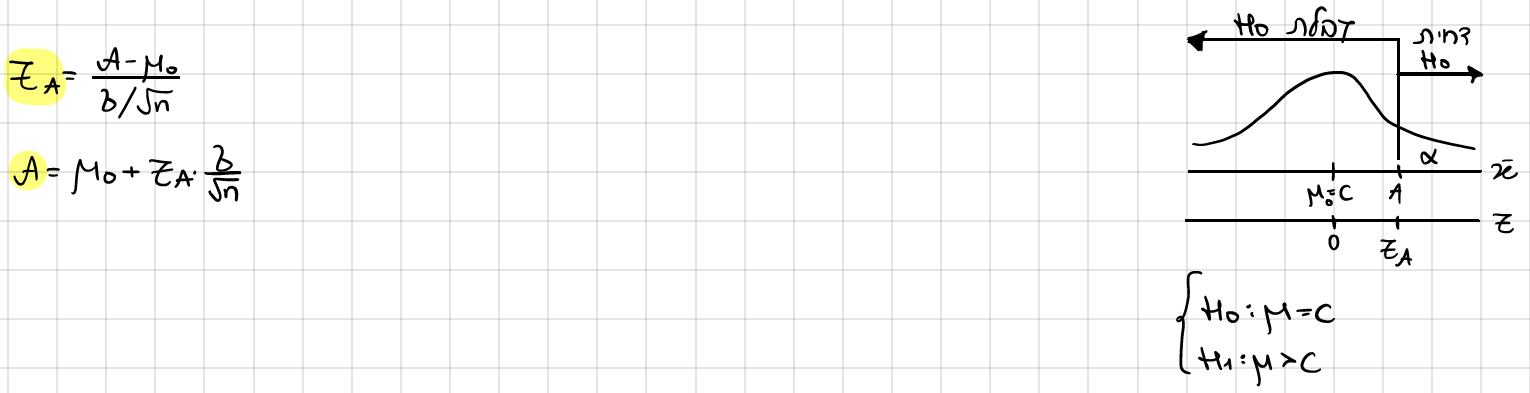
2 - חישוב ציון תקן לכלל ההכרעה לפי H1
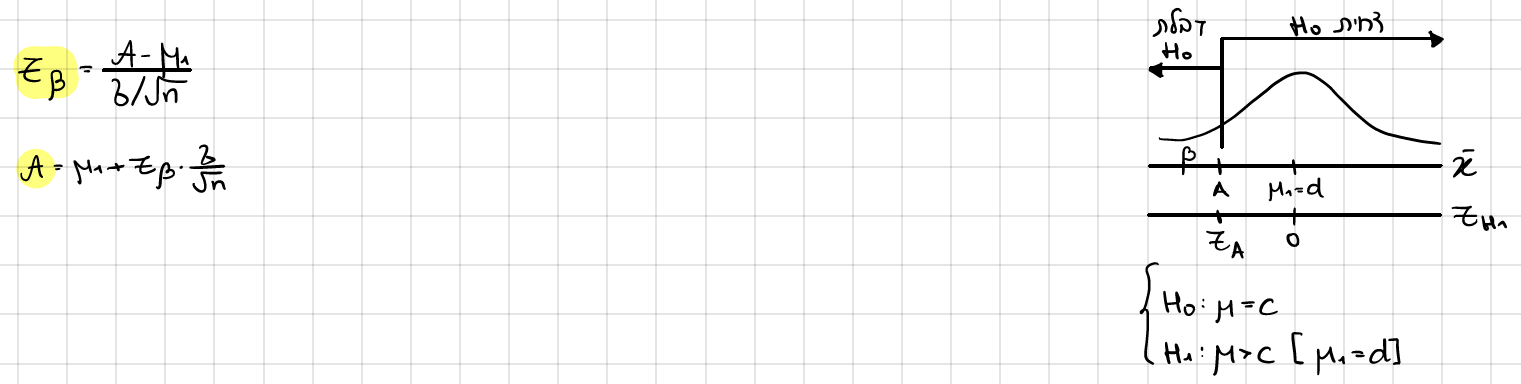
3 - חישוב טעות מסוג 2 לפי טבלה נורמלית, ציור וטבלת Z
כלל ההכרעה בציוני גלם לפי H0 ו-a
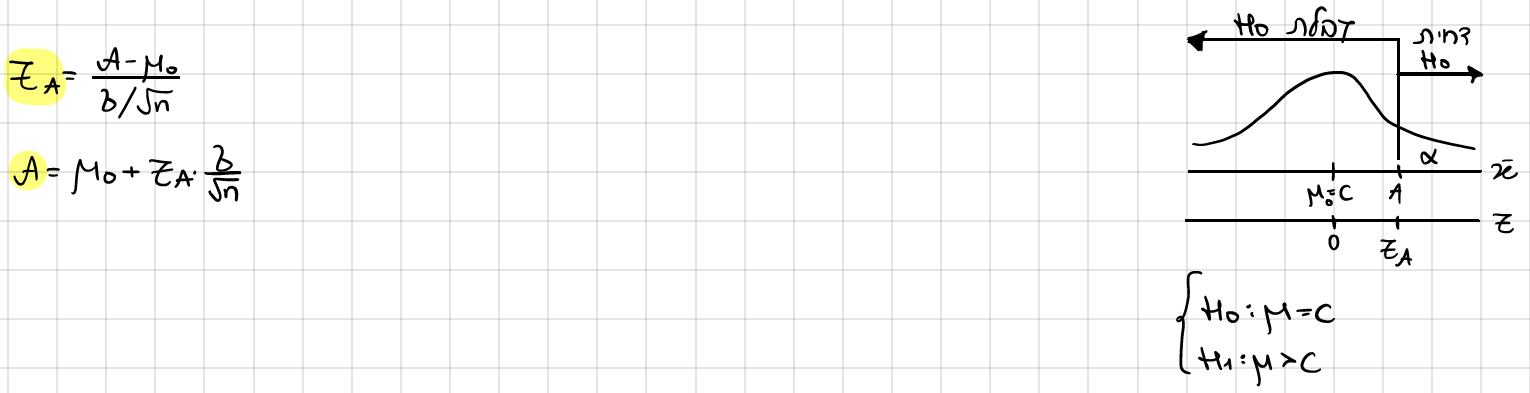
2 - חישוב ציון תקן לכלל ההכרעה לפי H1
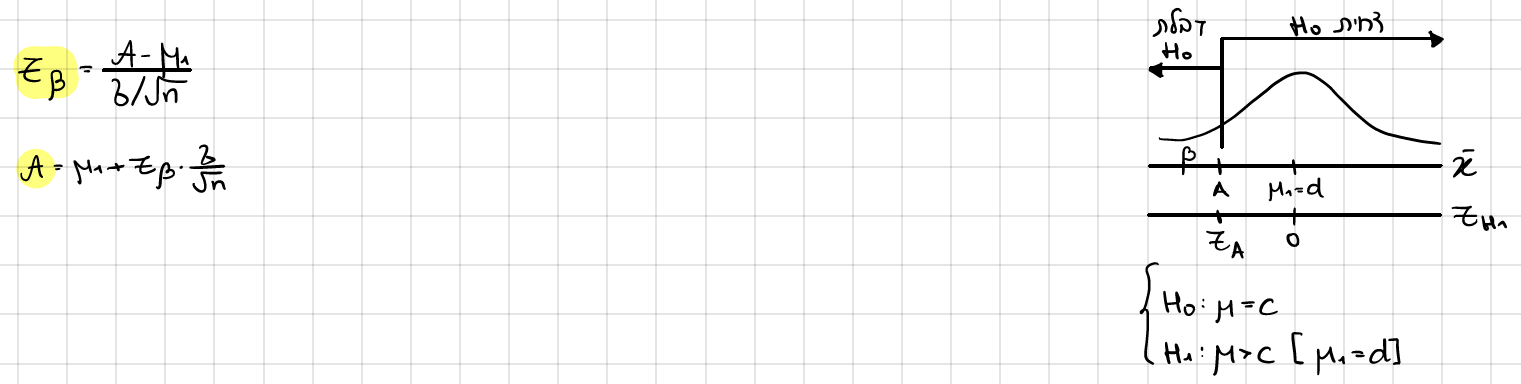
3 - חישוב טעות מסוג 2 לפי טבלה נורמלית, ציור וטבלת Z
נוסחה לחישוב גודל מדגם מינימלי בהינתן טעות

תרגיל - משרד הבריאות
מנתוני משרד הבירואת ידוע כי ממוצע לחץ הדם באוכלוסיה הוא 133 עם סטיית תקן 15.
במטרה לבדוק את הטענה כי מנהלים סובלים מלחץ דם גבוה יותר משאר האוכלוסיה נלקח מדגם מקרי של 64 מנהלים ונמצא שממוצע לחץ הדם שלהם 137.
טבלת נתונים:

מה תהיה מסקנתך ברמת מובהקות של 0.01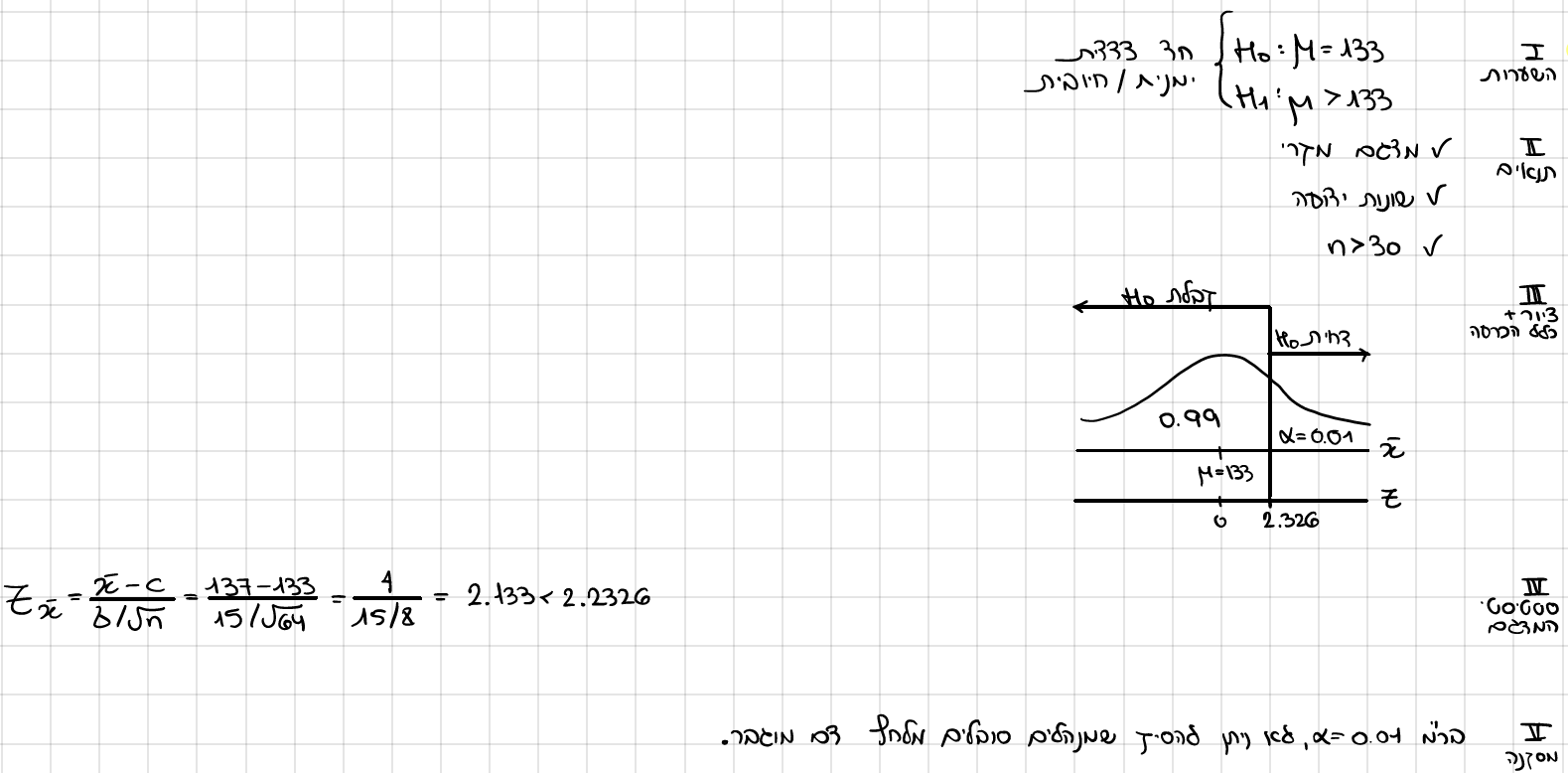
מהי הטעות האפשרית במסקנתך מסעיף א', אם ידוע שבקרב מנהלים לחץ הדם הממוצע הוא 140? הסבר וחשב


חשב גודל מדגם מינימלי כך שיבטיח שאם לחץ הדם בקרב המנהלים הוא אכן 140 נצליח לגלות זאת בהסתברות של 99% לפחות, ואם לחץ הדם אצל מנהלים אינו גבוהה מ133 יוחלט בטעות שהוא גבוה יותר בהסתברות שלא תעלה על 0.02
במטרה לבדוק את הטענה כי מנהלים סובלים מלחץ דם גבוה יותר משאר האוכלוסיה נלקח מדגם מקרי של 64 מנהלים ונמצא שממוצע לחץ הדם שלהם 137.
טבלת נתונים:

מה תהיה מסקנתך ברמת מובהקות של 0.01

מהי הטעות האפשרית במסקנתך מסעיף א', אם ידוע שבקרב מנהלים לחץ הדם הממוצע הוא 140? הסבר וחשב


חשב גודל מדגם מינימלי כך שיבטיח שאם לחץ הדם בקרב המנהלים הוא אכן 140 נצליח לגלות זאת בהסתברות של 99% לפחות, ואם לחץ הדם אצל מנהלים אינו גבוהה מ133 יוחלט בטעות שהוא גבוה יותר בהסתברות שלא תעלה על 0.02

תרגיל - רעידות אדמה
מתקן לבדיקת רעידות אדמה מפעיל התראה למצב חירום על סמך החוזק של 9 אותות שהוא קולט.
חוזר האותות מתפלג נורמלית.
במצב רגיל, תוחלת החוזק היא 5000 יחידות וסטיית תקן 900 יחידות.
במצב חירום, תוחלת החוזק היא 6300 יחידות וסטיית תקן נשארת 900.
המתקן מפעיל את ההתראה רק כאשר העוצמה הממוצעת של תשעת האותות עולה על 5600 יחידות.
טבלת נתונים:
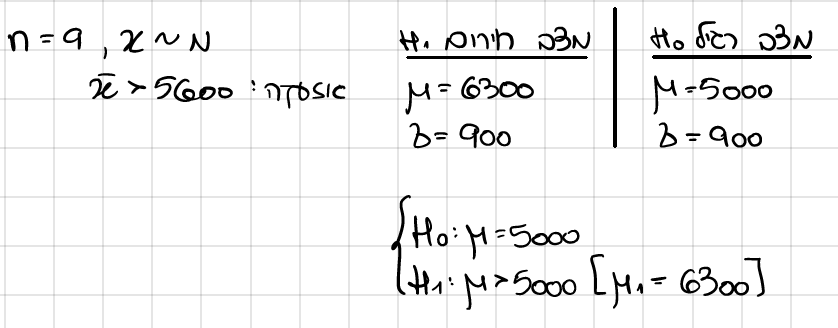
מהי ההסתברות של התראת שווא?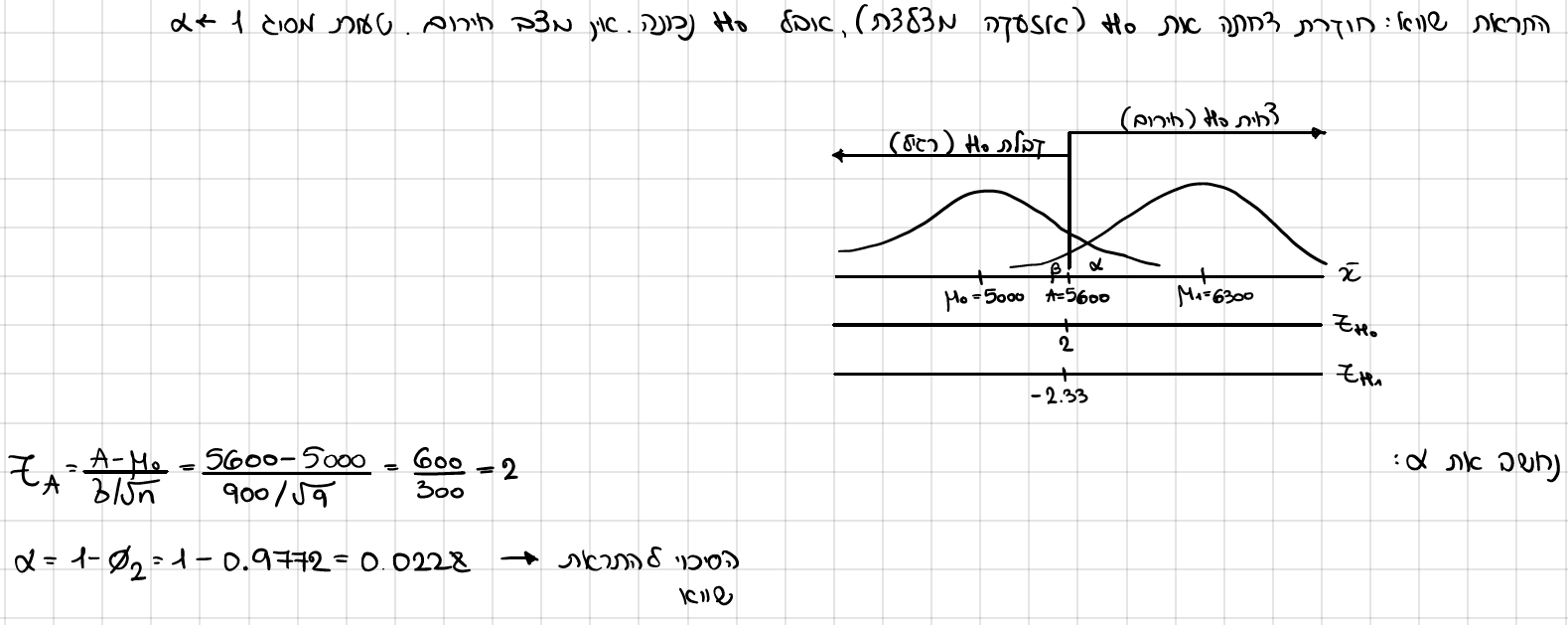
מהי ההסתברות שלא תופעל התראה במצב חירום?
ענה ללא חישוב, כיצד יושפעו הסתברויות הסעיפים הקודמים:
- מתקן ההתראה יופעל כאשר ממוצע החוזר יעלה ל5700 יחידות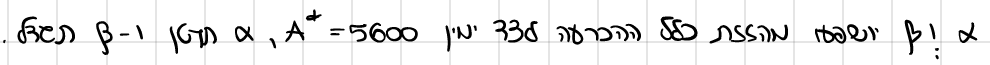 - מספר האותות הנקלטים יהיו 12
- מספר האותות הנקלטים יהיו 12 - תוחלת החוזק במצב חירום תהיה 6400 יחידות
- תוחלת החוזק במצב חירום תהיה 6400 יחידות
חוזר האותות מתפלג נורמלית.
במצב רגיל, תוחלת החוזק היא 5000 יחידות וסטיית תקן 900 יחידות.
במצב חירום, תוחלת החוזק היא 6300 יחידות וסטיית תקן נשארת 900.
המתקן מפעיל את ההתראה רק כאשר העוצמה הממוצעת של תשעת האותות עולה על 5600 יחידות.
טבלת נתונים:
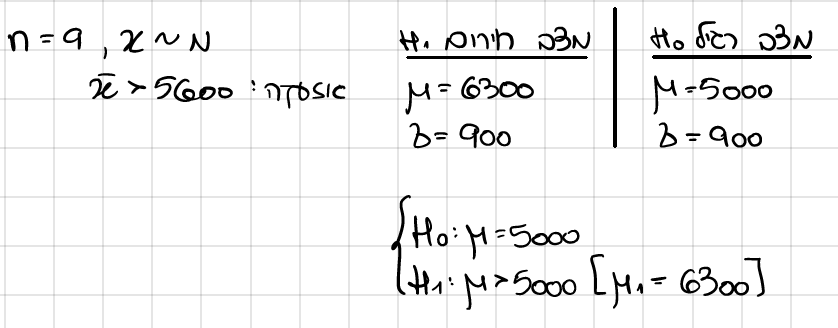
מהי ההסתברות של התראת שווא?

מהי ההסתברות שלא תופעל התראה במצב חירום?

ענה ללא חישוב, כיצד יושפעו הסתברויות הסעיפים הקודמים:
- מתקן ההתראה יופעל כאשר ממוצע החוזר יעלה ל5700 יחידות
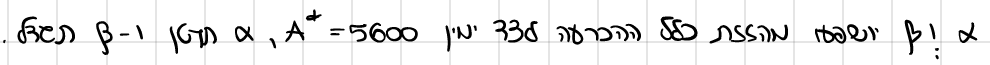 - מספר האותות הנקלטים יהיו 12
- מספר האותות הנקלטים יהיו 12 - תוחלת החוזק במצב חירום תהיה 6400 יחידות
- תוחלת החוזק במצב חירום תהיה 6400 יחידות
תרגיל - ייצור מוצר
הזמן הדרוש לייצור מוצר מסוים הוא בממוצע 10 שעות וסטיית תקן של זמני הייצור הוא שעה 1
בית חרושת טוען שיש לו תהליך יצור מהיר יותר.
נערכה בדיקה ונמצא ש-100 מוצרים נוצרים במשך 960 שעות.
טבלת נתונים: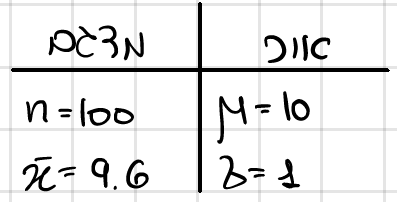
האם מוצדקת טענת בית החורשת? בדוק ברמת מובהקות של 0.05
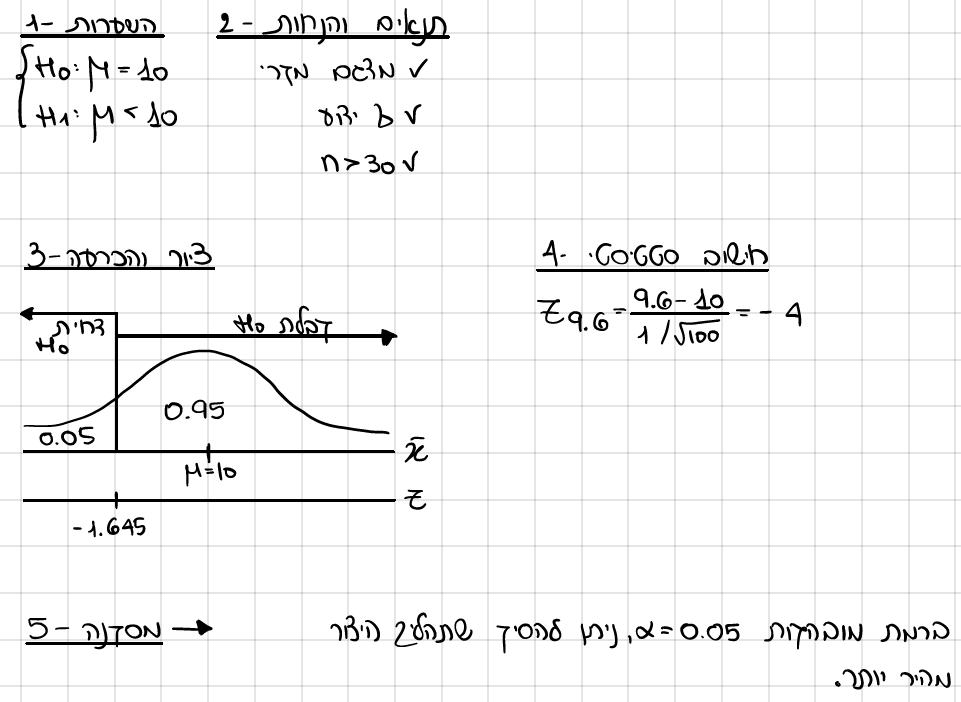
מהי הטעות האפשרית במסקנתך מסעיף א ומה ערכה? נמק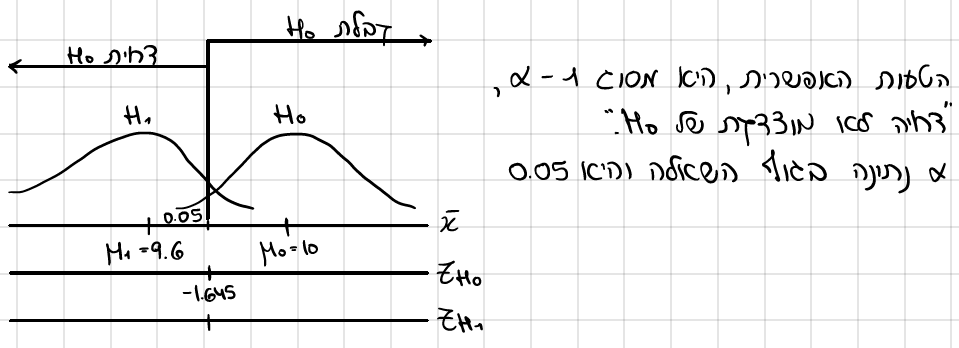
אם ידוע כי זמן היצור בבית החרושת הנ"ל הוא 9.8, מה הסיכוי שנצליח לגלות זאת? כיצד נקראת הסתברות זו ומה ערכה?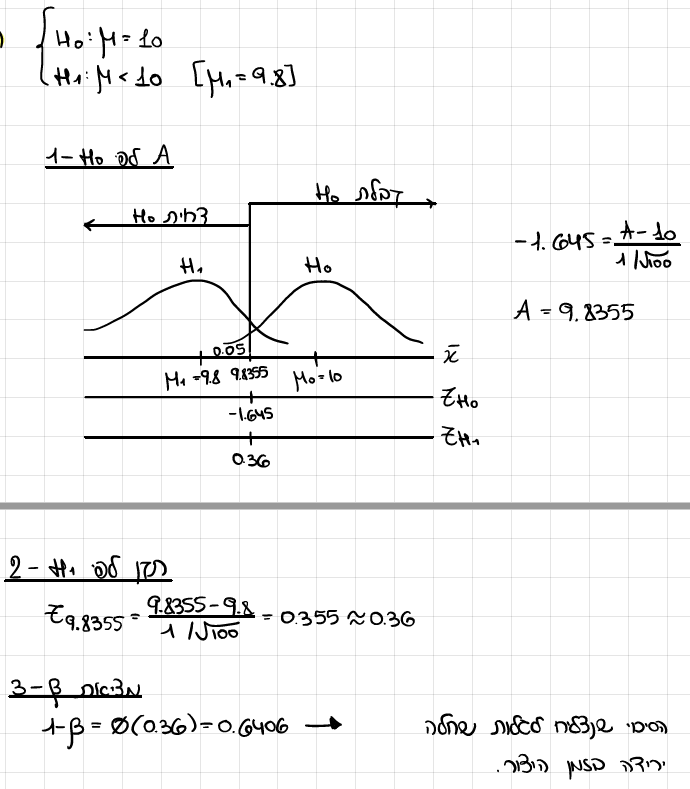
חשב גודל מדגם מינימלי כך שיבטיח שהסיכוי לדחייה לא מוצדקת של H0 לא יעלה על 0.02, והסיכוי לקבלה שגויה של H0 לא יעלה על 0.05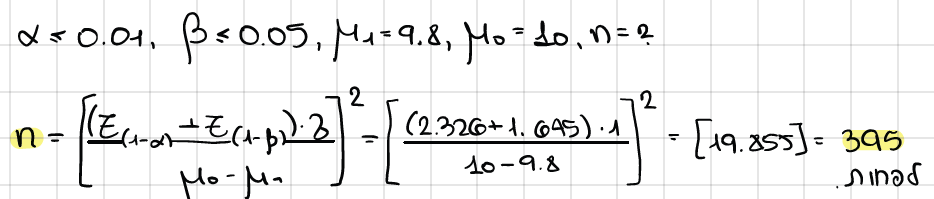
בית חרושת טוען שיש לו תהליך יצור מהיר יותר.
נערכה בדיקה ונמצא ש-100 מוצרים נוצרים במשך 960 שעות.
טבלת נתונים:
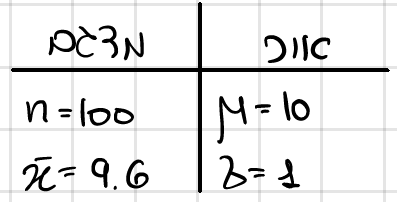
האם מוצדקת טענת בית החורשת? בדוק ברמת מובהקות של 0.05

מהי הטעות האפשרית במסקנתך מסעיף א ומה ערכה? נמק

אם ידוע כי זמן היצור בבית החרושת הנ"ל הוא 9.8, מה הסיכוי שנצליח לגלות זאת? כיצד נקראת הסתברות זו ומה ערכה?

חשב גודל מדגם מינימלי כך שיבטיח שהסיכוי לדחייה לא מוצדקת של H0 לא יעלה על 0.02, והסיכוי לקבלה שגויה של H0 לא יעלה על 0.05
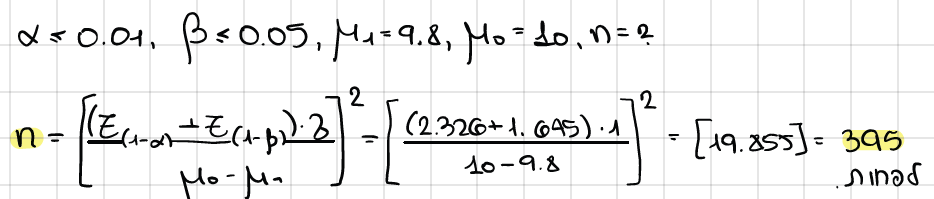
תרגיל - זמן ייבוש
משך זמן הייבוש ( תחת תנאים קבועים ) של צבע מסוים לעץ, מתפלג נורמלית עם תוחלת 90 דקות וסטיית תקן 10 דקות.
כימאי הציע תוסף לצבע שמטרתו לקצר את משך זמן הייבוש.
לבדיקת התוסף נלקח מדגם מקרי של 14 פלטות עץ שנצבעו בצבע עם התוסף.
הוחלט שאם משך הזמן הממוצע יהיה נמוך מ-85.6 דקות, יועננס השימוש בסתוסך, הכרוך בהוצאה כבדה.
נסח השערות וחשב רמת מובהקות של המבחן שבו משתמש היצרן.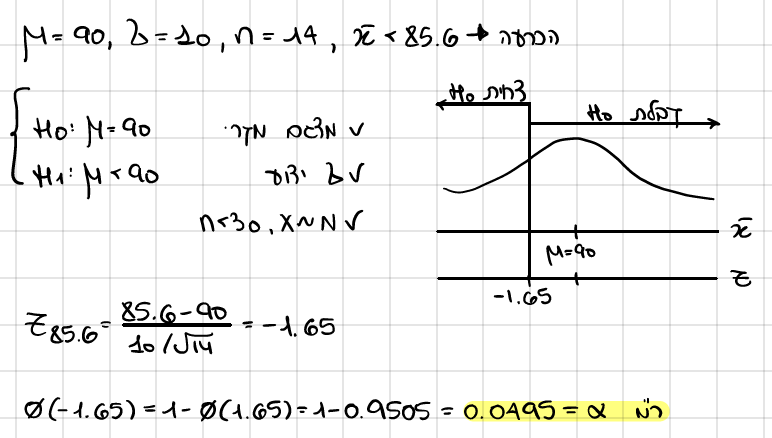
אם אומנם התוסף מקצר את תוחלת זמן הייבוש ב-4 דקות, מה ההסתברות שהדבר לא יתגלה.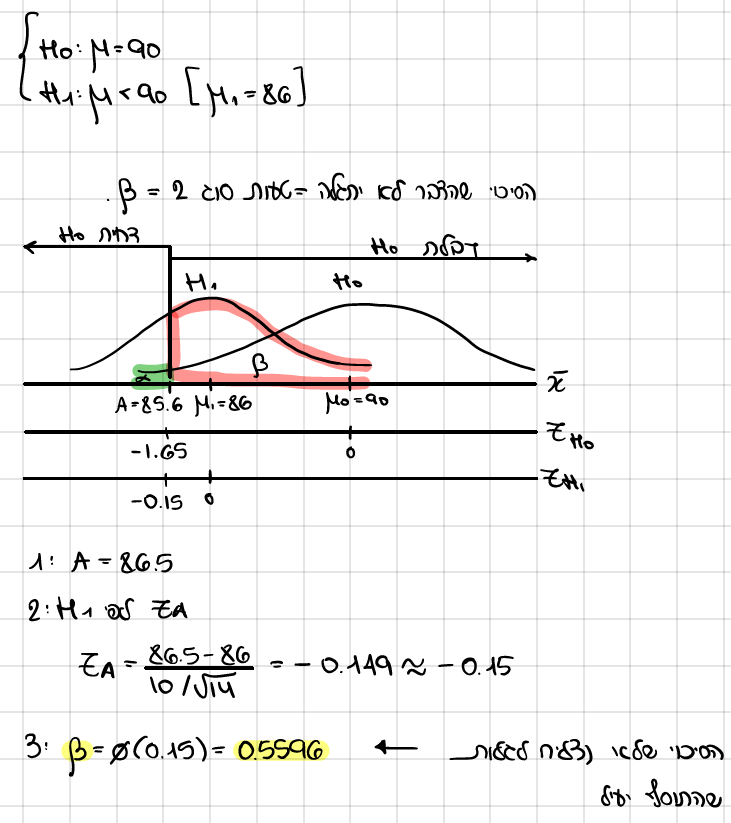
כמה פלטות יש לצבוע, כדי שאם התוסף אכן מקצר את תוחלת זמן הייבוש ב-4 דקות, הדבר יתגלה בהסתברות של 0.9 לפחות?
כימאי הציע תוסף לצבע שמטרתו לקצר את משך זמן הייבוש.
לבדיקת התוסף נלקח מדגם מקרי של 14 פלטות עץ שנצבעו בצבע עם התוסף.
הוחלט שאם משך הזמן הממוצע יהיה נמוך מ-85.6 דקות, יועננס השימוש בסתוסך, הכרוך בהוצאה כבדה.
נסח השערות וחשב רמת מובהקות של המבחן שבו משתמש היצרן.

אם אומנם התוסף מקצר את תוחלת זמן הייבוש ב-4 דקות, מה ההסתברות שהדבר לא יתגלה.

כמה פלטות יש לצבוע, כדי שאם התוסף אכן מקצר את תוחלת זמן הייבוש ב-4 דקות, הדבר יתגלה בהסתברות של 0.9 לפחות?

תרגיל - אלגוריתמים
הזמן לניתוח אלגוריתמים מתמטיים בשיטה קיימת מתפלג נורמלית עם ממוצע 6 שעות וסטיית תקן 2.
מתמטיקאי הציע שיטה חדשה שלטענתו מקצרת בשעה ניתוחים מסוג זה, מבלי לשנות את סטיית התקן.
השיטה החדשה נוסתה על ידי 25 מתמטיקאים מנוסים, שנבחרו באופן מקרי, ונמצא כי ההסתברות לגלות שאכן חל שיפור זה היא א0.9
מצא הסתברות לטעות מסוג ראשון של המבחן הסטטיסטי שנבדק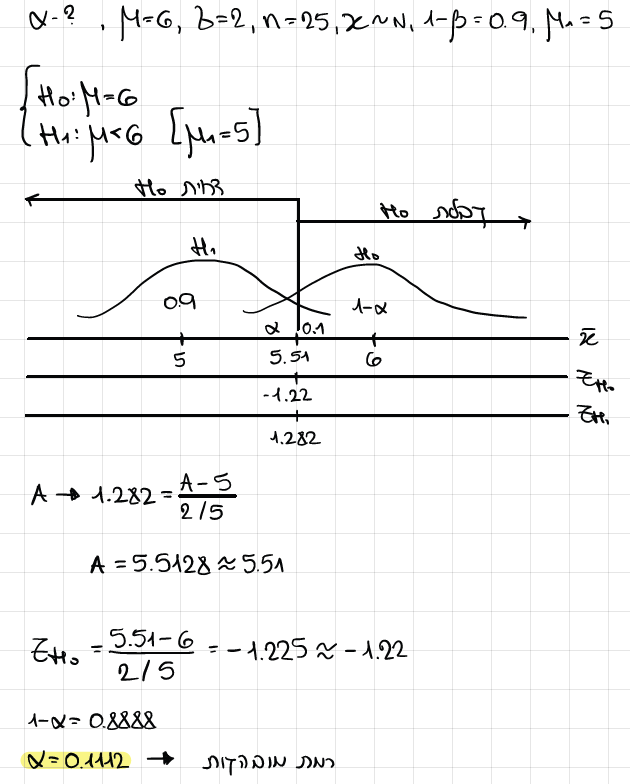
הממוצע שהתקבל במדגם היה 5.5. מה תהיה מסקנת הבדיקה? הסבר ללא חישוב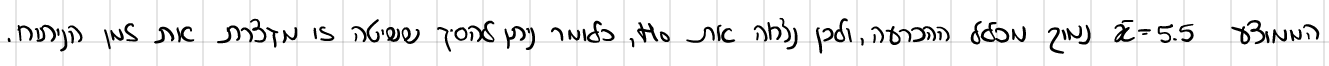
מהי מובהקות התוצאה? חשב והסבר.
מתמטיקאי הציע שיטה חדשה שלטענתו מקצרת בשעה ניתוחים מסוג זה, מבלי לשנות את סטיית התקן.
השיטה החדשה נוסתה על ידי 25 מתמטיקאים מנוסים, שנבחרו באופן מקרי, ונמצא כי ההסתברות לגלות שאכן חל שיפור זה היא א0.9
מצא הסתברות לטעות מסוג ראשון של המבחן הסטטיסטי שנבדק

הממוצע שהתקבל במדגם היה 5.5. מה תהיה מסקנת הבדיקה? הסבר ללא חישוב
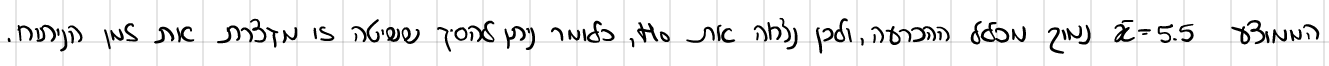
מהי מובהקות התוצאה? חשב והסבר.

תרגיל - משקעים
כמות המשקעים היומית באזור השרון מתפלגת נורמלית.
בשני רגילות עם תוחלת 16 מ"מ וס"ת 4, בשנת בצורת עם תוחלת 13 ואותה ס"ת.
סוכן ביטוח, המשטח את החקלאים בביטוח בצורת, מציע לחקלאים להגיש תביעה אם ב25 הימים הראשונים בחודש ינואר כמות המשקעים הכללית היתה מתחת ל350 מ"מ.
מהי רמת המובהקות של כלל ההכרעה שקבע סוכן הביטוח?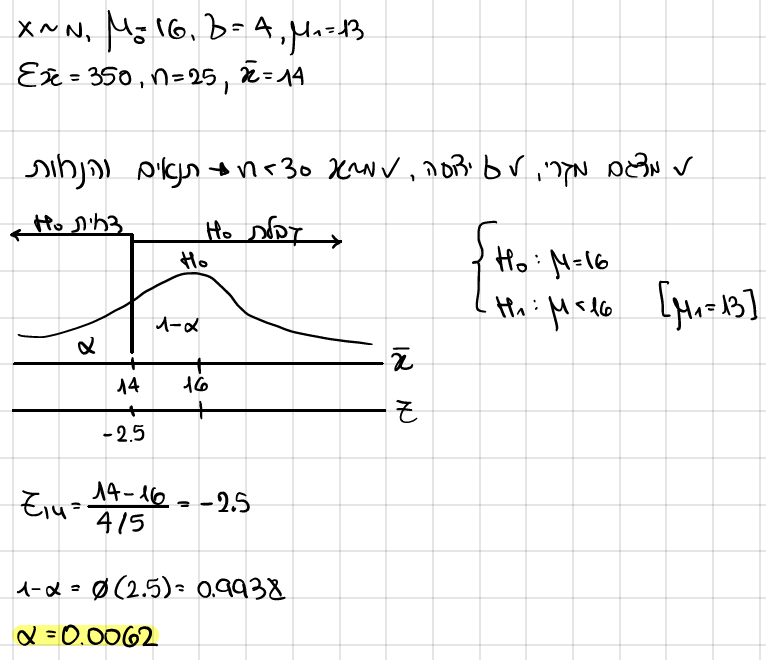
חשב הסתברות שנצליח לגלות זאת אם ר"מ 2.5%? כיצד נקראת הסתברות זאת?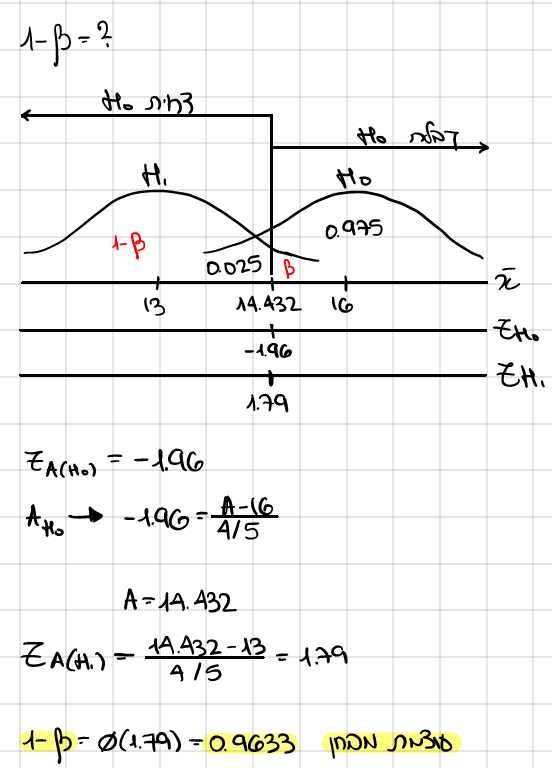
אם התקבל, בתקופה שנבדקה ממוצע של 14.5 מ"מ ליום, מהי רמת המובהקות הקטנה ביותר שעבורה יוחלט שמדובר בשנת בצורת?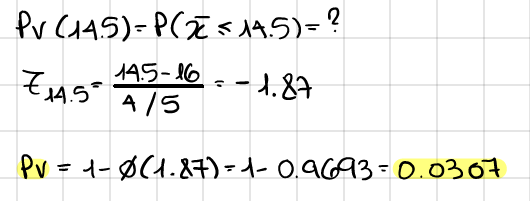
בהמשך לסעיף קודם, מה תהיה מסקנתך בר"מ 0.05? הסבר ללא חישוב נוסף
בשני רגילות עם תוחלת 16 מ"מ וס"ת 4, בשנת בצורת עם תוחלת 13 ואותה ס"ת.
סוכן ביטוח, המשטח את החקלאים בביטוח בצורת, מציע לחקלאים להגיש תביעה אם ב25 הימים הראשונים בחודש ינואר כמות המשקעים הכללית היתה מתחת ל350 מ"מ.
מהי רמת המובהקות של כלל ההכרעה שקבע סוכן הביטוח?

חשב הסתברות שנצליח לגלות זאת אם ר"מ 2.5%? כיצד נקראת הסתברות זאת?

אם התקבל, בתקופה שנבדקה ממוצע של 14.5 מ"מ ליום, מהי רמת המובהקות הקטנה ביותר שעבורה יוחלט שמדובר בשנת בצורת?
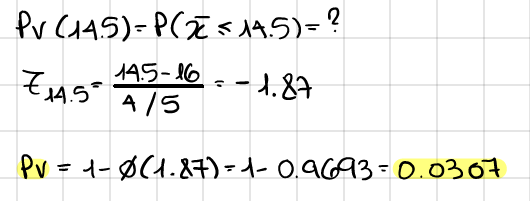
בהמשך לסעיף קודם, מה תהיה מסקנתך בר"מ 0.05? הסבר ללא חישוב נוסף

תרגיל - מאזניים
יש לבדוק אם מאזניים חדשים שהגיעו למעבדה מכוילים היטב.
לשם כך נלקחה כמות חומר במשקל ידוע ששווה ל100 גרם, ונשקלה 25 פעמים במאזניים החדשים ונתקבל ממוצע של 106 במדגם.
לפי פרסומי היצרן של המאזניים, ידוע בשקילת 100 גרם קיימת סטיית תקן של 16 גרם.
בדוק את הטענה שהמאזניים מכוילים היטב ברמת מובהקות 0.05.
מה הסיכוי שלא נצליח לגלות שמאזניים לא מכוילים היטב, אם ידוע שקיימת הטיה של 8 גרם כלפי מעלה?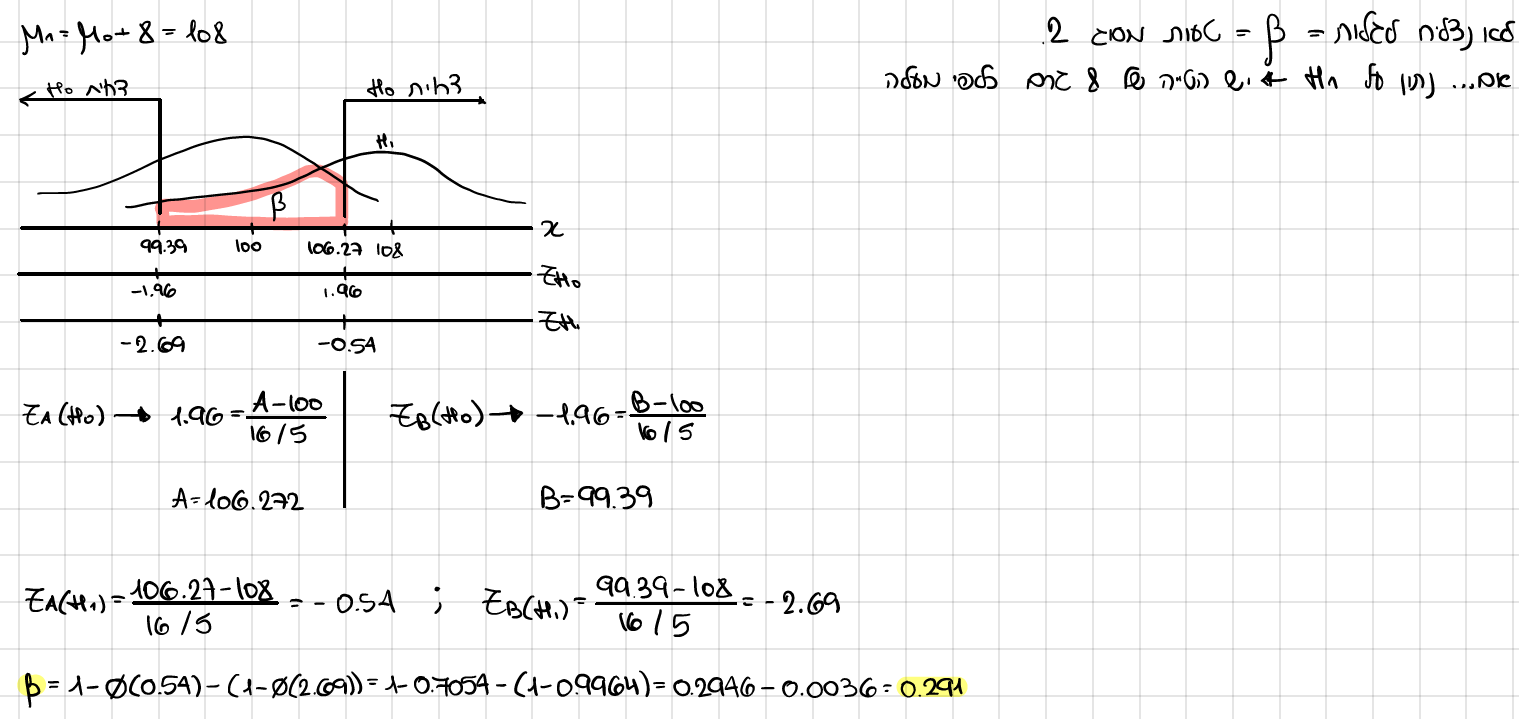
לשם כך נלקחה כמות חומר במשקל ידוע ששווה ל100 גרם, ונשקלה 25 פעמים במאזניים החדשים ונתקבל ממוצע של 106 במדגם.
לפי פרסומי היצרן של המאזניים, ידוע בשקילת 100 גרם קיימת סטיית תקן של 16 גרם.
בדוק את הטענה שהמאזניים מכוילים היטב ברמת מובהקות 0.05.

מה הסיכוי שלא נצליח לגלות שמאזניים לא מכוילים היטב, אם ידוע שקיימת הטיה של 8 גרם כלפי מעלה?

